DÉRIVÉES PARTIELLES (ÉQUATIONS AUX) - Analyse microlocale

DÉRIVÉES PARTIELLES (ÉQUATIONS AUX) - Analyse microlocale

Soit P un opérateur différentiel sur un ouvert 行 de Rⁿ , P = a 見(x ) D^x 見. | 見| 諒m

Son symbole principal:

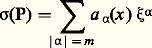s’interprète, si l’on fait un changement de coordonnées sur 行, comme une fonction sur T 行, le fibré cotangent à 行. Si P est à «caractéristiques réelles simples», par exemple si P est l’opérateur des ondes, il est connu depuis longtemps (Hadamard, Leray) que certaines singularités de l’équation homogène Pu = 0 se propagent suivant la projection sur 行 des «courbes bicaractéristiques» de P, les courbes intégrales dans T 行 du champ hamiltonien:

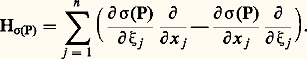Cependant l’idée de traiter les opérateurs différentiels dans l’espace T 行 (l’espace de phase des physiciens) ne s’impose qu’à partir de 1965 (Maslov), et surtout 1969-1970 (D. F. Egorov, M. Sato, L. Hörmander), et c’est Sato qui a l’idée en 1969 de considérer les singularités d’une distribution ou d’une hyperfonction sur 行 comme la projection (la superposition) des singularités d’un nouvel objet, les microfonctions, défini naturellement sur T 行, et de travailler directement dans cet espace. Ce sont ces idées que nous allons décrire, ainsi que quelques-unes de leurs applications, mais de manière évidemment très superficielle. Nous insisterons surtout sur la théorie analytique plutôt que sur la théorie différentiable. Bien que les idées directrices soient essentiellement les mêmes, les outils employés sont différents: fonctions de variables complexes dans la première, transformée de Fourier dans la seconde.

1. Hyperfonctions, microfonctions, front d’onde

Soit 行 un ouvert de l’espace Rⁿ , 臨 un cône ouvert convexe de Rⁿ . On appelle «tuboïde» de base 行 de profil 臨 un ouvert 行 de Cⁿ tel que pour tout ouvert 行 說 說 行, tout cône 臨 tel que ( 臨 惡 S^n-1 ) 說 說 ( 臨 惡 S^n-1 ), il existe un voisinage 輪 de 行 dans Cⁿ avec ( 行 + i 臨 ) 惡 輪 說 行. Mikio Sato a défini en 1959-1960 les hyperfonctions sur 行 comme somme de valeurs au bord de fonctions holomorphes: une telle hyperfonction u sur 行 s’écrit u = b (f ⁱ ), I fini, où i 捻 If ⁱ est holomorphe dans un tuboïde de base 行 de profil 臨ⁱ , b désigne la valeur au bord «formelle », avec la relation d’équivalence: b (f ⁱ ) = 0 s’il existe des fonctions g ⁱ ,^j i 捻 Iholomorphes dans les tuboïdes de profils 臨^{i ,j} , enveloppe convexe de 臨ⁱ 聆 臨^j , avec:

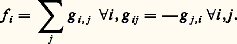On construit ainsi le faisceau B des hyperfonctions sur Rⁿ , qui contient le faisceau des distributions et qui a la propriété remarquable d’être flasque: une hyperfonction sur 行 se prolonge à Rⁿ tout entier. La relation d’équivalence utilisée par Sato dans la définition précédente traduit le théorème de l’edge of the wedge , qui est une généralisation du théorème du tube de Bochner (cf. Prolongement analytique , in FONCTIONS ANALYTIQUES - FONCTIONS ANALYTIQUES DE PLUSIEURS VARIABLES COMPLEXES): soit 臨¹ et 臨² des cônes convexes de Rⁿ et f continue sur ( 塚¹ + i Rⁿ ) 聆 ( 塚² + i Rⁿ ), analytique à l’intérieur (en général non convexe) de cet ensemble; alors f se prolonge en une fonction analytique dans l’intérieur de l’enveloppe convexe de cet ensemble. La version plus générale portant sur des distributions au lieu de fonctions continues et la version locale sont vraies également.

On définit le spectre singulier d’une hyperfonction sur 行 en précisant les directions qui interviennent dans sa décomposition en somme de valeurs au bord. Si x 捻 行, 﨡 捻 i T^x ( 行) est un vecteur «conormal» à Rⁿ dans Cⁿ au point x avec 﨡 0, on dira que (x , i 﨡) n’appartient pas au spectre singulier de u (en abrégé SS(u )), si, au voisinage de x , u s’écrit:

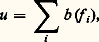f ⁱ holomorphe dans un tuboïde de profil 臨ⁱ , 﨡 n’appartenant pas au polaire du cône 臨ⁱ . On peut ainsi construire un faisceau (le faisceau C des microfonctions) sur T^Rn Cⁿ , le fibré conormal à Rⁿ dans Cⁿ , dont les sections globales sont les hyperfonctions sur Rⁿ , le spectre singulier d’une hyperfonction étant le support de la microfonction associée. On peut aussi généraliser ces constructions en remplaçant Rⁿ par une variété analytique réelle M, Cⁿ par un complexifié X de M. Une théorie analogue est développée presque simultanément par L. Hörmander dans le cas différentiable. Si u est une distribution sur Rⁿ , on dit que (x , 﨡) n’appartient pas au front d’onde de u (en abrégé WF(u )), si, 﨏 étant une fonction C size=1^秊 à support compact égale à 1 au voisinage de x , la transformée de Fourier de 﨏u est à décroissance rapide dans un voisinage conique de la direction 﨡.

Par exemple, si 嗀 est la masse de Dirac à l’origine, i (SS( 嗀)) = WF( 嗀) =0 憐 Rⁿ . Si f est la fonction C size=1^秊 qui vaut e size=1^{漣1/x 2} pour x 捻 R, x 礪 0, et 0 pour x 麗 0, SS(f ) =(x , i 﨡); x = 0, et WF(f ) est vide. Signalons que les constructions de M. Sato utilisent les outils très puissants de la cohomologie des faisceaux et des catégories dérivées, mais que l’on peut aussi utiliser une variante de la transformée de Fourier pour calculer le spectre singulier (J. Bros-D. Iagolnitzer).

2. Opérateurs microdifférentiels

La théorie des opérateurs pseudodifférentiels ou microdifférentiels s’intègre parfaitement aux nouveaux concepts que nous venons d’introduire. Décrivons-la dans le cadre analytique.

Soit X un ouvert de Cⁿ , 輪 un ouvert de TX, (z , 﨣) les coordonnées sur TCⁿ . Un opérateur microdifférentiel holomorphe P sur 輪 se représente comme une somme formelle:

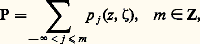les p ^j étant des fonctions holomorphes sur 輪, homogènes de degré j 捻 Z en 﨣 et vérifiant la condition: pour tout compact K 說 輪, il existe t 礪 0 tel que la série:

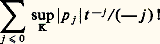soit convergente.

On définit la composition de deux opérateurs microdifférentiels en étendant la formule de Leibniz:

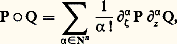et l’on définit ainsi un faisceau d’anneaux non commutatifs, 劉^X sur TX. Si P est d’ordre m :

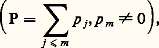on appelle p ^m son symbole principal; si celui-ci ne s’annule pas sur un ouvert 律 de TX, il existe un unique opérateur Q sur 律 tel que P 獵 Q = Q 獵 P = 1. Comme les opérateurs différentiels sur X définissent des opérateurs microdifférentiels sur TX (on représente l’opérateur P par e size=1^{漣麗z ,} size=1^﨣 size=1^礪 P(e size=1^{麗z ,} size=1^﨣 size=1^礪), la loi de composition étant respectée), on peut considérer 劉^X comme une «localisation» du faisceau 阮^X des opérateurs différentiels. Nous décrirons plus loin les propriétés algébriques de ce faisceau d’anneaux.

Le faisceau 劉^X opère naturellement sur le faisceau C^M des microfonctions (ici M est un ouvert de Rⁿ , X un voisinage de M dans Cⁿ ). Pour décrire cette action, supposons que la microfonction u soit la valeur au bord d’une fonction holomorphe f dans un tuboïde de profil 臨, le polaire de 臨 étant un voisinage suffisamment petit de la direction dx ⁿ = (0, ..., 1), et soit P un opérateur microdifférentiel au voisinage de (x ^o; idx ⁿ ). On peut alors développer P en série de Taylor:

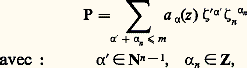et si H désigne l’hyperplan complexe d’équation z ⁿ = ih , associer à P l’opérateur intégro-différentiel P^H:

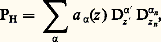D^{-l z n} (f ) désignant la l -ième primitive de f nulle à l’ordre l sur H, pour l 閭 0. On constate alors que P^H(f ) est holomorphe dans un tuboïde au voisinage de x ^o, et b (P^H(f )), sa valeur au bord, ne dépend pas du choix de H au voisinage de (x ^o; idx ⁿ ), car P^H(f ) 漣 P ^H size=1(f ) (H désignant un hyperplan z ⁿ = ik ) est holomorphe au voisinage de x ^o.

3. Transformations canoniques et distributions lagrangiennes

Si M est une variété (réelle ou complexe), TM son fibré cotangent est naturellement muni d’une 1-forme 諸 qui, en coordonnées (x ) = (x ¹, ..., x ⁿ ) sur M, (x , 﨡) sur TM, s’écrit:

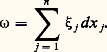La forme d 諸 est bilinéaire alternée non dégénérée, et établit donc en chaque point p 捻 TM un isomorphisme H entre T^P TM et T^P TM. Si f est une fonction sur un ouvert de TM, le champ hamiltonien H^f est par définition le champ de vecteur image réciproque de df par l’isomorphisme H. Par exemple, si f = 靖(P), on retrouve le champ de vecteurs décrit dans l’introduction. Si f et g sont deux fonctions sur un ouvert de TM, leur crochet de Poisson est la fonction:

Soit N une autre variété, de même dimension que M, 律 un ouvert de TN. Une transformation canonique 﨏 de 輪 ouvert de TM sur 律 est un isomorphisme (différentiable, analytique réel, ou analytique complexe suivant la catégorie dans laquelle on travaille) de 輪 sur 律, homogène pour la structure fibrée sur M et N, et qui échange les l-formes: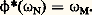

Si l’on note 炙 size=1^﨏 le graphe de 﨏 dans 輪 憐 律 et 炙^a size=1^﨏=(x ,y ; 﨡;n );(x ,y ; 﨡; 漣 兀) 捻 炙 size=1^﨏, la variété 炙^a size=1^﨏 est lagrangienne dans 輪 憐 律, c’est-à-dire involutive (si deux fonctions s’annulent sur 炙^a size=1^﨏, leur crochet de Poisson aussi) et de dimension minimale (1/2 dim ( 輪 憐 律)). Un résultat fondamental (datant des années 1970) est que, localement, on peut toujours «quantifier» une transformation canonique, c’est-à-dire trouver 﨏 isomorphisme du faisceau C^M| 輪 sur C^N| 律 et un isomorphisme (encore noté 﨏) de 劉^X| 輪 sur 劉^Y| 律 (ici M et N sont des variétés analytiques réelles de complexifiées X et Y), ces isomorphismes étant compatibles à l’action de 劉^X sur C^M et de 劉^Y sur C^N et vérifiant:

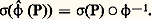En particulier, les transformations canoniques quantifiées conservent les notions de spectre singulier et de front d’onde.

Les transformations canoniques quantifiées jouent donc dans les équations aux dérivées partielles le rôle des difféomorphismes dans la géométrie différentielle.

Exemple . La transformation de Legendre qui à (x , 﨡) associe (y , 兀) = 﨏(x , 﨡), où 﨡ⁿ 0, 兀ⁿ 0, y ^j = 﨡^j 﨡^{n -1}, 兀^j = 漣 x ^j 﨡ⁿ (j 麗 n ), y ⁿ = 麗x , 﨡 礪 﨡^{n -1}, 兀ⁿ = 﨡ⁿ , peut être quantifiée si l’on pose:

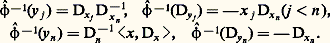La construction de 﨏 utilise une classe particulièrement importante de microfonctions que nous allons décrire dans le cadre C size=1^秊: ce sont les distributions lagrangiennes (on dit aussi distributions de Fourier). Soit 炙 une variété lagrangienne conique dans un ouvert de TRⁿ , en dehors de la section nulle. On peut trouver (localement sur 炙) une fonction réelle 﨏(x , ) sur Rⁿ 憐 R^N, homogène en , non dégénérée en , c’est-à-dire telle que les différentielles des (face=F0019 煉 﨏)/(face=F0019 煉 ⁱ ) soient linéairement indépendantes sur 臨 size=1^﨏 =(x , ); 﨏 size=1 = 0 et pour laquelle:

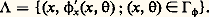Soit a (x , ) une fonction C 秊 à support dans un voisinage conique en d’une direction de 臨 size=1^﨏, et telle que pour un m 捻 Z, C 閭 0:

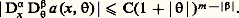La distribution lagrangienne (associée à la phase 﨏 et au symbole a d’ordre 諒 m ) est définie formellement par:

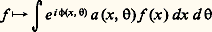(on lui donne un sens en intégrant par parties en ), et la méthode de la phase stationnaire montre que le front d’onde de cette distribution est contenu dans 炙.

Une étude plus finie de ces distributions fait intervenir le «fibré de Maslov» sur 炙, qui rend compte de ce que la projection de TM sur M n’est pas de rang constant sur 炙 (phénomène des caustiques en optique géométrique). Une telle étude s’avère nécessaire dans des calculs de spectre d’opérateurs (Maslov, Leray), ces calculs ayant d’ailleurs été en partie à l’origine de cette théorie.

4. Propagation des singularités

Considérons par exemple l’opérateur des ondes:

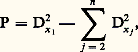et plaçons-nous au voisinage d’un point (x ⁰, 﨡⁰) 捻 T Rⁿ , avec 﨡⁰ 0, 靖(P)( 﨡⁰) = 0. On sait depuis Darboux qu’une transformation canonique permet d’échanger au voisinage de 﨡⁰ la fonction 靖(P) et a 﨡¹, avec a (x ⁰, 﨡⁰) 0. En «quantifiant» cette transformation, on peut alors échanger P avec un opérateur microdifférentiel E(D¹ + R), E étant inversible et R d’ordre 0. Comme l’on montre facilement que l’opérateur D¹ + R peut être échangé (par composition par des opérateurs inversibles) avec D¹, on voit que l’équation Pu = 0 est «microlocalement», c’est-à-dire au voisinage de (x ⁰, 﨡⁰), équivalente à une équation D¹v = 0. On comprend alors pourquoi les singularités de u se propagent le long des bicaractéristiques de P, puisque celles-ci sont invariantes par transformation canonique, et que c’est évidemment le cas des solutions de l’équation D¹v = 0.

Ce résultat de propagation a été largement étendu et le rôle des bicaractéristiques complexes commence à être compris. En particulier, la généralisation des distributions de Fourier à des variétés lagrangiennes complexes a été entreprise (Melin, Sjöstrand), et la géométrie de ces variétés au voisinage du réel joue un rôle crucial dans les questions de résolubilité ou d’hypo-ellipticité analytique. Mais ce sont dans les problèmes aux limites que les résultats de propagation se révèlent les plus intéressants et débouchent sur des applications physiques (diffusion, problème inverse). Un rayon lumineux, par exemple, peut en effet s’interpréter comme une singularité d’une solution élémentaire de l’opérateur des ondes, singularité portée par une courbe bicaractéristique de cet opérateur. Dans le cas où ces rayons sont transverses à un «miroir », on démontre facilement un théorème de réflexion des singularités, mais, si le miroir est courbe et si l’on étudie le comportement d’un rayon «rasant», on démontre qu’il y a diffraction, c’est-à-dire propagation dans le bord (le miroir), pour les singularités analytiques et pas pour les singularités différentiables (Friedlander, Melrose, Sjöstrand).

5. Systèmes

L’anneau des opérateurs différentiels à coefficients variables n’est pas commutatif, et c’est sans doute cet obstacle (essentiellement psychologique) qui fait que ce n’est qu’à partir des années 1970 (I. N. Bernstein, M. Kashiwara) que l’on traite les systèmes d’équation aux dérivées partielles avec les outils de la géométrie algébrique. Ces outils, associés à ceux de la microlocalisation, ont permis à M. Sato, M. Kashiwara et T. Kawaï d’obtenir des résultats spectaculaires sur les systèmes, en particulier leur classification générique.

Le faisceau 劉^X des opérateurs microdifférentiels sur TX, le fibré cotangent à une variété analytique complexe X, est un faisceau d’anneaux non commutatifs, unitaire, cohérent et noethérien à droite et à gauche, filtré par l’ordre des opérateurs. À un système d’équations microdifférentielles:

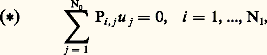on associe le 劉^X-module à gauche 紐, conoyau de la matrice (P) = (Pⁱ ,^j ). Les solutions du système () dans un faisceau 杻 (sur lequel 劉^X opère à gauche) s’identifie naturellement à 流om size=1^劉X(face=F0021 紐, 杻), l’ensemble des homomorphismes 劉^X-linéaires à gauche de 紐 dans 杻, et l’obstruction à résoudre le système:

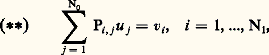quand les vⁱ satisfont aux conditions de compatibilités

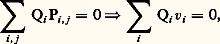est décrite par le groupe 劉xt ¹ size=1^劉X (face=F0021 紐, 杻). (Ces généralités s’appliquent évidemment à tout système d’équations A-linéaire à gauche sur un anneau ou faisceau d’anneaux A.) On définit alors la variété caractéristique du système comme le support du module 紐, et de nombreux résultats sur les équations aux dérivées partielles peuvent alors être formulés et résolus, pour les systèmes. On peut, par exemple, résoudre le problème de Cauchy pour les systèmes hyperboliques (M. Kashiwara-P. Schapira). Un résultat essentiel de la théorie est que la variété caractéristique d’un système est un ensemble analytique involutif de TX. En particulier, sa codimension est inférieure ou égale à la dimension de X. Quand celle-ci est maximale, on dit que le système est «holonôme»; et la théorie de Fuchs a été généralisée à ces systèmes (P. Deligne, M. Kashiwara, T. Kawaï) et des liens très profonds sont apparus avec la géométrie algébrique et la théorie des groupes (résolution de la conjecture de Kazdan-Lutzig par J.-L. Brylinski-Kashiwara).

Encyclopédie Universelle. 2012.